In this blog post, I want to briefly explain what the replication crisis in economics is and what are its most likely causes. I'll then provide some evidence along with personal stories and anecdotes that illustrate the bad behaviors that generate the replication crisis. Then, I'm going to detail the set of solutions that I think we need in order to overcome the crisis. Finally, I will end with a teaser about a project that I am preparing with some colleagues, the Social Science Knowledge Accumulation Initiative, or SKY (yeah, I pronounce SSKAI SKY, can I do that?), that we hope is going to provide the infrastructure necessary in order to implement the required changes.
In a sense, I'm relieved and happy that this crisis occurs, because it is high time that we put the great tools of the empirical revolution to good use by ditching bad practices and incentives and start accumulating knowledge.
What is the replication crisis?
The replication crisis is the fact that we do not know whether the published empirical results could be replicated if one tried to reproduce them exactly in the same way as the original authors did, with the same data collection procedure and the same statistical tools.
The replication crisis come from editors choosing to only publish studies that show statistically significant results. Because statistically significant results can be obtained by chance or by using Questionable Research Practices (QRPs), the published record is populated by studies whose results are due to luck or to data wizardry.
The replication crisis is a very bad problem because it implies that there is no guarantee that the truth will emerge from the published record. When published results are selected in order to find effects that are just big enough to pass the infamous statistical significance thresholds, then the published record is going to be severely biased. Small effects are going to look bigger than they really are, zero effects (or very small effects) might look like they exist and are substantial. And we do not know which effects are concerned and how many of them there is. The replication crisis means that we cannot trust the published empirical record in economics.
The Four Horsemen of the Apocalypse: the Behaviors Behind the Replication Crisis
Before getting to the evidence, let me detail the four behaviors that make the published record unreliable: publication bias, the file drawer problem, p-hacking and HARKing. Let me describe them in turn with the help of an example.
Let's start with publication bias. Imagine that you have a theory saying that all coins are biased. The theory does not say the direction of the bias, only that all coins are biased, some might give more heads than tails and others more tails than heads. In order to test the theory, 100 research teams start throwing coins, one for each team. By sheer luck, sometimes, even unbiased coins will have runs with more heads than tails or more tails than heads. How do you decide whether the run is due to sheer luck or to a biased coin? Well, scientists rely on a procedure called a statistical test. The idea is to assume a balanced coin (we call that the Null Hypothesis) and derive what type of data we should see under that assumption. The way it works is a follows: assuming a fair coin, the distribution of let's say the proportion of heads over runs of N flips is going to be centered around 0.5, with some runs giving a larger probability than 0.5, and some runs giving a lower probability. The distribution is going to be symmetric around 0.5, with tails that get thinner and thinner as we move away from 0.5 on each side because we are less likely to obtain 75% of heads than 55%. Now, the test works like this: each team compares its own proportion of heads to the theoretical distribution of the proportion of heads under the Null for a sample of size N. If the observed proportion of heads is far away in the tails of this distribution, on either side, we are going to say that the coin is biased, because it is unlikely that its run comes from the fair coin Null distribution. But how do we decide precisely? By convention, we decide that the assumption that the coin is unfair is going to be statistically significant if it is such that the proportion of heads over N runs is equal or higher to the 97.5 percentile of the distribution of the fair coin under the Null or equal to or smaller than the 2.5 percentile of the same distribution. Why do we choose these values? Because they have the property that, under the Null, we are only going to conclude incorrectly that a coin is biased while it is actually fair 5% of the time, and 5% is considered a small quantity, or, rather, it was chosen by the inventor of the procedure, Ronald Fisher, and it kind of became fetishized after that. Something like a papal decree (we have a lot of them in science, rather surprisingly). The precise values of the thresholds above or below which we are going to decide that a coin is not fair depend on sample size. They are closer to 0.5 as the number of flips increases, because with a larger number of flips, more and more samples are going to find values closer to 0.5 under the Null Hypothesis that the coin is fair. With larger sample sizes, a smaller deviation is going to be considered more surprising.
Even if all coins are fair, and the theory is wrong, by the sheer property of our testing procedure, 5 out of the 100 competing teams are going to report statistically significant evidence in favor of the biased coin theory: 2.5 that the coin is biased towards heads and 2.5 that the coin is biased towards tails. That would be fine if all the 100 teams reported their results. The distribution of the proportion of heads over the 100 teams would be very similar to the distribution under the null, and would thus invalidate our theory and vindicate the Null.
But, what would happen if only the statistically significant results get published? Well, The published record would only contain evidence in favor of a false theory, invalidating the correct Null hypothesis: the published record would say "All coins are unfair."
Waouw, how is it possible that something like that happens? It seems that my colleagues and friends, who are referees and editors for and readers of scientific journals, hate publishing or reading about Null non-significant results. Why is that? You might say that it looks completely foolish to do so once I've presented you with how the procedure works. Sure, but I came with what I hope is a clear understanding of the problem after a lot of effort, reading multiple books and articles about the replication crisis, simulating these coin tosses for myself, teaching that problem in my class and writing a series of blog posts on the topic. (i) Most scientists do not have a great mastery of statistical analysis (well, you already have to master your own discipline, and now you would need stats on top of that, that's obviously hard). The statistical education of scientists is a series of recipes to apply, and of rules to follow, instead of an introduction to the main issue (that of sampling noise) and to the ways to respond to it. As a consequence of poor statistical training, most scientists interpret Null results as inconclusive, and statistically significant results as conclusive. (ii) Most scientists are not really aware of the aggregate consequences of massive science, with multiple teams pursuing the same goal, and how that interacts with the properties of statistical tests. Most teams have not read John Ioannidis' paper on this (on which my example is loosely based). (iii) Researchers are like every other human being on the planet, they like a good story, they like to be surprised and entertained, they do not like boring. And most correct results are going to be boring: “Coins are fair? Boring! Who would like to know about that? Wait, what, coins are unfair? Here is the front page for you, buddy!” The problem is that the world is probably mostly boring, or, stated otherwise, most of our theories are probably false. We are thus going to find a lot of Null results and we should know about them in order to weed out the wrong theories.
OK, now we understand publication bias. But there’s more. Scientists understand that editors and referees do not like insignificant results. As a consequence, they adopt behaviors that make the replication crisis more severe. These Questionable Research Practices (QRPs) - the file drawer problem, p-hacking and HARKing - increase the likelihood of finding a significant effect even if there is none to levels much higher than 5%, sometimes to levels as high as 60%. As a consequence, the published record is populated by zombie theories even if the truth is actually the good old Null hypothesis. The file drawer problem is scientists simply not even bothering to convert non significant results into papers because they know they’ll never get to publish them. As a consequence, the bulk of evidence in favor of the Null is eradicated before even getting to the editors. The second problem is called p-hacking. P-hacking is when researchers use the degrees of freedom that they have in experimental design in order to increase the likelihood of finding significant results. And there are unfortunately tons of ways to do just that. In my biased coin theory example, p-hacking could happen for example if researchers checked periodically the result of the test after a few coin flips, and then after collecting a few more, and decided to stop collecting data when the test result becomes significant. Researchers might also decide to exclude some flips from the sample because they were not done in correct conditions. This might look very innocent and might not be done in bad faith: you’re just doing corrections to your data when your result is non significant and stop doing most of them when they are. Finally, scientists might try out a host of various tests of the hypothesis and report only the statistically significant results. For example, bias could be defined as the proportion of heads being different from 0.5, but it could also be that the coin has long runs of successive heads or of successive tails, even if it is unbiased on average. Or it might be that the coin is biased only when tossed in a certain way. If all teams try all these combinations and only report the statistically significant results, the proportion of the 100 teams finding significant results would increase by a lot, sometimes up to 60, instead of the initial 5. HARKing or Hypothesizing After the Results are Known is the procedure or formalizing the theory after seeing the data and reporting it as if the theory came first. For example, over the 100 team investigating coin fłips, the ones finding significantly more heads might end up publishing a paper with evidence in favor of a theory stating that coins are all biased towards heads. The other teams might publish a paper with evidence in favor of the theory that all coins are biased towards tails. Some teams might find that coins produce successive “hot hands” runs of heads or tails, some teams might publish evidence for theories that the way you throw the coin makes a difference on how biased the coins are, etc. Don’t laugh, that has happened repeatedly.
What is the evidence that the published record in economics is tainted by publication bias and Questionable Research Practices?
If my theory of the replication crisis is correct, what should we see? Well, it depends on whether we spend our time hunting for true effects or for Null effects. More precisely, it depends on the true size of the effects that we are hunting for and on the precision of our tests (i.e. the size of our samples). If we spend our time looking for small, very small or zero effects with low precision, i.e. low sample size, we should see the distribution under the null, but truncated below the significance thresholds if there is publication bias. That is, we should see only significant results being published, with the bulk of them stacked closer to the statistical significance threshold and then the mass slowly thinning as we move to higher values of the test statistics. If there is p-hacking or HARKing, we should see a bulging mass just above the significance thresholds. On the contrary, if we mostly are looking at large effects with large sample sizes, the distribution of test statistics should look like a normal only slightly censored on the left, where the missing mass of non-significant results fall. We should have a small bulging mass above the significance threshold if there is p-hacking or HARKing, but that should not be the main mass. The main mass should be very far away from the significance thresholds, providing undisputable evidence of large and/or precisely estimated effects.
So what do we see? The following graph is taken from a very recent working paper by Abel Brodeur, Nikolai Cook and Anthony Heyes. It plots in black the distribution of 13440 test statistics for main effects reported in 25 top economics journals in 2015, by method (I'll come back to that). It also reports the theoretical distribution under the Null that all results are zero (interrupted grey line) and the thresholds above which the effects are considered to be statistically significant (vertical lines).
What we see is highly compatible with researchers hunting mostly for Null effects, of massively missing Null effects and of published effects due either to luck or to QRPs.
- There is no evidence of large and/or precisely estimated effects: in that case, test statistics would peak well above the significance thresholds. In the actual data, it's all downhill above the significance thresholds.
- We might interpret the plot for IV as evidence of medium-sized or not super precisely estimated effects. Taken at face value, the peak around the significance thresholds of IV might tell the story of effects whose size places them just around the significance thresholds with the precision that we have in economics. That interpretation is very likely to be wrong though:
- It just is weird that our naturally occurring effects just happen to align nicely around the incentives that researchers face to get their results published. But, OK, let's accept for the moment that that's fate.
- Editors let some Null results pass, and actually there are too many of them. As a consequence, the distribution is not symmetric around the main effect, and the bulge is too sharp around the significance thresholds, and the mass of results at zero is too big to be compatible with a simple story of us hunting down effects that are exactly around detection thresholds.
- The quality of the evidence should not depend on the method. IV seems to provide evidence of effects, but the much more robust methods RDD and RCT show much less signs of a bulge around significance thresholds. It could be that they are used more for hunting Null effects, but it is hard to believe that users of IV have a magic silver bullet that tells them in advance where the large effects are, while RCT and RDD users are more stupid. No, most of the time, these are the same people. The difference is that it's much harder to game an RCT or an RDD.
- We see clear evidence of p-hacking or HARKing around significance thresholds, with a missing mass below the thresholds and an excess mass above. It is clearly apparent in RCTs, tiny in RDDs, huge in DID and so huge in IV that it actually erases all the mass until zero!
OK, so my reading of this evidence is at best extremely worrying, at worst completely damning: yes, most statistically significant published results in economics might very well be false. There is no clear sign of undisputable mass of precisely estimated and/or large effects far above the conventional significance thresholds. There are clear tell-tale signs of publication bias (missing mass at zero) and of p-hacking and HARKing (bulge around significance thresholds, missing mass below). So, we clearly do not know what we know. And we should question everything that has been published so far.
Some personal anecdotes now that are intended to illustrate why I'm deeply convinced that the evidence I've just presented corresponds to the worst case scenario:
- I p-hacked once. Yes, I acknowledge that I have cheated too. It is so innocent, so understandable, so easy, and so simple. I had a wonderful student that did an internship with me. He was so amazing, and our idea was so great, we were sure we were going to find something. The student worked so hard, he did an amazing job. And then, the effect was sometimes there, sometimes not there. We ended up selecting the nicely significant effect and published it. I wanted to publish the finding for the student. I also was sure that our significant effect was real. I also needed publications, because this is how my output is measured, and at the time I did not understand very well the problem of publication bias and how severe it was. I chose to send the paper to a low tier journal though, in order not to claim this paper too much on my resume (it is not one of my two main papers). Yes, it was a little bit of a half-assed decision, but nobody's perfect ;)
- After that, I swore never to do it again, I felt so bad. I put in place extremely rigorous procedures (RCTs with preregistration, publication of everything that we are doing, even Null results, no selection of the best specifications). And, mind you, out of my 7 current empirical projects, 5 yield non-significant results.
- After presenting preliminary non-significant results at the first workshop of my ANR-funded project, a well-intentioned colleague told me that he was worried about how I was going to publish. "All these non significant results, what are you going to do about them?" he said. He said it like it was a curse or a bad omen that I had so many insignificant results. He is an editor. It almost felt like I was wasting public research funds on insignificant results, a problem I could not foresee before starting with the study. But see the problem: if I cannot convert my research in published results, I am going to fail as a researcher and to fail to raise more money to do my future research. But in order to publish, I need significant results, which are beyond my control, unless I start behaving badly and pollute the published empirical record with tainted evidence. This is the incentive structure that all of us are facing and it is deeply wrong.
- Turns out my colleague was right: the editor of the first journal we sent a paper with a non significant result wrote back "very well conducted study, but the results are insignificant, so we are not going to publish it." I kid you not.
- I asked in a seminar to the presenter whether he obtained his empirical results before or after crafting his theory. He looked at me puzzled. Took a long time to think about his answer and then said: "Do you know anyone who formulates theories before seeing the data?" I said "Yes, people who pre-register everything that they are doing." He replied "Is that a sin not to do it?" I said "It's kind of a sin, it's called HARKing. The main thing that I want to know is whether the evidence in favor of your theory came before or after your theory. It is much more convincing if it came after."After talking more with him, he could delineate which results inspired his theoretical work and which ones he obtained after. But he was unaware that presenting both sets of results on the same level was a QRP called HARKing (and I'm not pointing fingers here, we are all ignorant, we all sinned).
- Recently on Twitter, a young researcher boasted that his large productivity in terms of published papers was due to the fact that he stopped investigating non-promising research projects early. If you stop at once when you have non-significant results, then, you contribute to the file drawer problem.
- One of the most important current empirical researchers in economics said in an interview “where we start out is often very far away from the papers that people see as the finished product. We work hard to try to write a paper that ex-post seems extremely simple: “Oh, it’s obvious that that’s the set of calculations you should have done.”” This leaves the possibility open that he and his team try out a lot of different combinations before zeroing in on the correct one, a behavior dangerously close to p-hacking or HARKing. I'm not saying that's what they do. I'm saying that no procedures ensure that they do not, and that the empirical track record in the field pushes us to lose trust when this kind of behavior is allowed.
- With my students last year, we examined roughly 100 papers in empirical environmental economics. I cannot fathom how many times we commented on a result that was like “the conclusion of this paper is that this policy saved 60000 lives plus or minus 60000.” The bewildered look in my students' eyes! “Then it could be anything?” Yes it could. And even more worrying, how come all of these results are all so close to the significance threshold? My students were all wondering whether they really could trust them.
- I cannot express how much people in my field are obsessed with publication. It seems to be the end goal of our lives, the only thing we can talk about. We talk more about publications than we talk about scientific research. Careers are made and destroyed based on publications. The content itself is almost unimportant. Publications! Top journals! As if the content of our knowledge would follow directly from competition for top publications. Hard to avoid pointing that neither Darwin nor Newton, nor Einstein considered publication to be more important than content. And hard to avoid saying that then we are only rewarding luck (the luck of finding the few significant results stemming out of our Null distributions) or worse, questionable research practices. And that we are polluting the empirical record of evidence and ultimately betraying our own field, science and, I'd say, shooting ourselves in the foot. Why? Because when citizens, policy-makers and funders will catch up with that problem (and they will), they will lose all confidence in our results. And they'll be right.
I hope now that you are as worried as I am about the quality of the empirical evidence in economics. Obviously, some people are going to argue that there is not such a problem. That people like me are just frustrated failed researchers that try to stifle the creativity of the most prolific researchers. How do I know that? It all happened before in psychology. And it is happening right now. There are people mocking Brodeur et al for using the very statistical significance tests that they claim are at the source of the problem (I let you decide whether this is an argument or just a funny deflection zinger. OK, it's just the latter). Some people point out that significant results are just results that signal that we need more research in this area, in order to confirm whether they exist or not. I think this is a more elaborate but eventually fully wrong argument. Why? For two reasons. First, it is simply not happening like that. When a significant result gets published, it is considered as the definitive truth, whether or not it is precise, close to the significance threshold or not. And there is NEVER an independent replication of that result. This is not seen as an encouragement for more research. It is just the sign that we have a new result out. Cases of dissent with the published record are extremely rare, worryingly rare. And the first published significant result now becomes an anchor for all successive results, a behavior already identified by Feynman in physics years ago that lead him to propose blind data analysis. Second, there are no incentives for doing so: replications just do not get attention, and have a hard time being published. If they find the same results: boring! If they don't, then why? What did the authors do that lead to a different result? No-one believes that sampling noise alone can be responsible for something as a change in statistical significance, whereas it is actually the rule rather than the exception, especially when results are very close to the significance threshold. Third, this is simply a waste of time, effort and money: all of these significant results stem from the selection of 5 significant results among 100 competing teams. Imagine all the time and effort that is going into that! We have just ditched the work of 95 teams just to reward the 5 lucky ones that obtained the wrong result! This simply is crazy. It is eve crazier when you add QRPs to the picture: following that suggestion, you just end up trying to reproduce the work of the sloppiest researchers. Sorry, I prefer to hunt down rigorously for Null effects all of my life than trying to chase the latest wild geese that some of my colleagues claim to have uncovered.
The existing solutions to the replication crisis
OK, so what should we do now? There are some solutions around that start being implemented. Here are some of the ones that I do not think solve the issue because they do not make the Null results part of the published record:
- Most referees of empirical research now require extensive robustness checks, that is trying out to obtain your results under various methods and specifications. This is in a sense a way to try to have you not do too much p-hacking, because a p-hacked result should disappear under this type of scrutiny. Actually, it is true, the most fragile p-hacked results might disappear, but some extreme results will remain, and some true results will disappear also. Or maybe we will see more p-hacking and HARKing around the robustness checks. It is actually an interesting question for Brodeur et al: do papers including robustness checks exhibit less signs of p-hacking. Note also that this approach will not make the record include Null results, just a more selected set of significant ones. So, as a consequence, it does not address the main issue of publication bias.
- Some people have suggested to decrease the threshold for statistical significance from 5% to 0.5%. We will still miss the Null results we need.
- Some people have suggested the creation of a Journal of Null results. Well, that's great in theory but if Null results have no prestige or impact because people do not read them, or use them, or quote them, then noone will send papers there. And we will miss the Null results.
- Some journals have started requiring that datasets be posted online along with the code. It will for sure avoid the most blatant QRPs and correct some coding mistakes but it will not populate the empirical record with the Null results that we need in order to really be sure of what we do know.
There are some solutions that are more effective because they make the track record of Null results accessible:
- The AEA recently created a registry of experiments. This is a great first step, because it obliges you to pre-register all your analysis before you do anything. No more QRPs with pre-registration. Pretty cool. Three problems with pre-registration. First, it is voluntary. to make it really work, we need both funders and journals to agree that pre-registration is a prerequisite before submitting a paper or spending money on experiments. Second, it does not solve publication bias. we still are going to see only the significant results get published. It helps a little because now we theoretically know the universe of all studies that have been conducted, if it is being made a pre-requisite, and we can estimate how many of them have been published eventually. If it is only 5%, we should just be super cautious. If it is also mandatory to upload your results on the registry, we could collect all these unpublished Null results and get a truthful answer. But that's with a lot of caveats. For the moment, it does not apply to methods other than RCTs: natural experiments (DID, IV, RDD) and structural models are never pre-registered.
- An ever better solution is that of registered reports. Registered reports are research proposals that are submitted to a journal and examined by referees before the experiment is run. Once the project is accepted, the journal commits to publish the final paper whatever the results, significant or not. That's a great solution. Several journals in psychology now accept registered reports, along with one in economics. The problem is that it is not really adapted to some field research where things are decided in great urgency at the last minute (it happens a lot when working with non research institutions).
- A great solution is simply to organize large replications of the most important results in the field. Psychologists have created the Psychological Science Research Accelerator (modeled after physicists CERN) and OSF where hundreds of labs cooperate in choosing and conducting large precise studies trying to replicate important results.
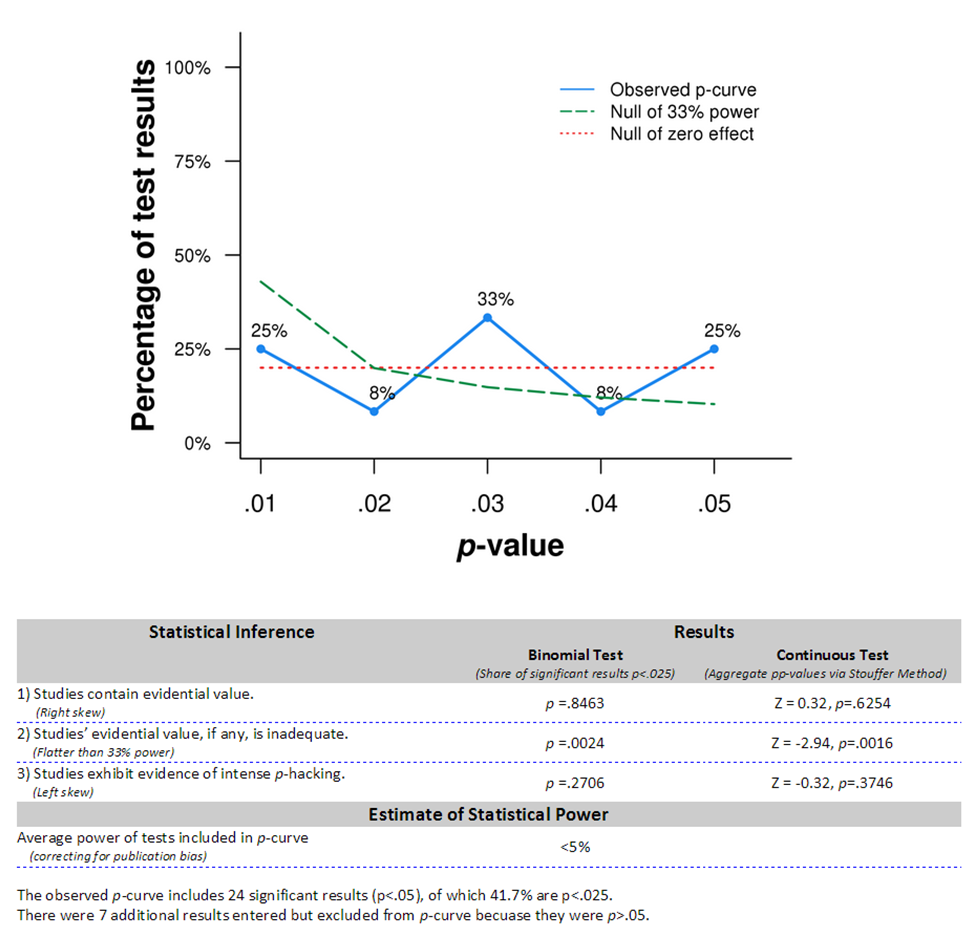
- A super cool solution is to start accumulating knowledge using meta-analysis. Meta-analysis simply aggregate the results of all the studies on the same topic. Meta-analysis can also be used to detect publication bias. First, you can compare the most precise results to the less precise ones. If the more precise results are smaller, that is sign of publication bias. It does not mean that the most precise results are not biased though. We would need pre-registered replications to say that. Second, you can also compare the distribution of the p-values of statistically significant results (it's called p-curving). It should be decreasing if there is a true effect (a super cool result), it is flat under the Null and it is increasing with QRPs, with a bulge just below significance thresholds. What if we were p-curving the Brodeur et al data? We'll probably just find huge signs of publication bias, because it is clear that there is a bulge, and the upward part of the distribution is compatible with the Null. It would be great if Abel and his coauthors could actually p-curve their data to confirm my suspicion.
What is the track record of these changes? Let's see what happened when doctors moved to registered reports: they moved from 57% of trials reporting a significant effet (i.e. an effective drug) to 8%!
When psychologists tried to replicate huge swaths of published findings, they found that 60% of them did not replicate.
When economists did the same (for a very small number of studies), they found 40% did not replicate, and effects where overestimated by a factor of 2! Below is a graph from a paper by Isaiah Andrews and Max Kasy where they propose methods for detecting and correcting for publication bias and apply their tools to the data from this replication. The blue lines are the original estimates and the black lines the ones corrected for publication bias. You can see that originally borderline statistically significant results (with the confidence interval caressing the 0 line) are actually containing zero and that most of the presented results contain zero in their confidence interval, and are thus compatible with zero or very small effects.
When meta-analyzing economics literatures, John Ionnanidis and his colleagues found huge signs of publication bias, with effects overestimated by a factor of 2 to 4! Below is a graph from their paper showing the distribution of the inflation factor due to publication bias. The mode of the distribution is 300% inflation, so effects that are 3 times too large. Note that this is a cautious estimate of the amount of publication bias that there is in these literatures, since it uses the most precise estimates as an estimate of the truth, while they might very well be biased as well.
My proposal: the Social Science Knowledge Accumulation Initiative (SKY)
The problem with all these changes is that they are voluntary. That is unless funders and journal editors decide to require preregistration for example, we will not see huge progress made on that front. What I'm proposing is to use meta-analysis to organize the existing literature, to evaluate the quality of the empirical published record bit by bit, and to use it to discipline fields, journals, universities and researchers by giving them the incentives to adopt the best research practices. This will be the first job of SKY. We are going to provide a tool that makes doing and reporting the results of meta-analysis easier.
What is nice with meta-analysis is that they summarize what we know and they help detect our likely biases. You can detect publication bias in a literature, obviously, but you can also apply p-curving to a journal, to an editor, to a university, a department, a team and even to an individual researcher. I'm not saying that we should, but the mere fact that we could should push everyone into adopting better practices. Moreover, it seems very hard to game meta-analysis and p-curving, because the only way to game them seems to me to be to expressly cheat.
The application of meta-analysis and p-curving to whole literatures should curb down the incentive for publication bias. Indeed, what will be judged passed on to policy-makers and students are the results of meta-analysis, and not the results of individual studies. Researchers should not compete for doing meta-analysis, they should cooperate. Anyone having published a paper included in the meta-analysis should be included as an author, that is they have incentive to disclose everything that they are doing (even Null results will be valued now), and incentives to control what their fellow researchers are doing, because their results are going to be on the paper as well.
Meta-analysis will also push us towards the normalization of methods, so that the quality of methods is controlled and standardized, in order for studies to be included in a meta-analysis. We also need replicators that redo the statistical analysis of each separate studies. Great candidates are master and PhD students in methods class, under the supervision of a PI.
We finally need a tool to make research more open that is more versatile than pre-registered reports. I propose to make all of our lab notes open. That is we will set up a researcher's log, where he reports everything that he is doing on a project. He will first start with the idea. Then he will report the results of the first analysis, or his pre-analaysis plan, and his iterations. That does not obviate the need for pre-registered reports, but it looks like a pre-registered report only less rigid. If the lab notes are made open, you can receive comments from colleagues at all stages in order to improve your analysis. I know that researchers are afraid of having their ideas stolen, but first this is a red herring (I still have to meet someone to whom it has actually happened, but I have met dozens of researchers who have heard of someone to whom it has happened). What better way not to be beaten to the post than publicizing your idea on a public time-stamped forum? This will also be a very effective way to find co-authors.
Some last few thoughts in the form of an FAQ:
- Why not use the existing infrastructure developed in Psychology such as the Accelerator? I see SKY as complementary to the Accelerator as a way to summarize all research, including the one conducted on the Accelerator. The Accelerator is extraordinary for lab research. Some empirical economists do some lab research (and we should probably do much more), but most of us do research using Field Experiments (FE, a.k.a. Randomized Controlled Trials (RCTs)), Natural Experiments (NE) or Structural Models (SM). The Accelerator is not super adapted to both FE and NE because it requires a very strict adherence to a protocol and a huge level of coordination that is simply not attainable in the short run in economics. When running FE, you have to choose features in agreement with the local implementers, most of the details are decided at the last minute. When using NE, we are tributary of the characteristics of the data, of the exact features of the Natural Experiment that we are exploiting and that are sometimes revealed only after digging deep in the data. My hope is that eventually, the coordination brought about by SKY around research questions will enable the gradual standardization of methods and questions that will enable us to run standardized FE and NE. SM are in general intending to predict the consequences of policies or reforms. Their evaluation will entail pre-registration of the predictions before seeing the data, or an access to the code so that anyone can alter the estimation and holdout samples.
- How does SKY contribute to the adoption of good research practices? My idea is that SKY will become the go-to site for anyone wanting to use results from economics research (and hopefully in the end eventually any type of research). Every result will be summarized and vetted by entire communities on SKY, so that the best up-to-date evidence will be there. Funders, policy-makers, journalists, students, universities, fellow researchers will come on SKY to know what is the agreed upon consensus on a question, if the evidence is sound, what are the unanswered questions, etc. Fields with a track record of publication bias will risk losing their funding, their positions, their careers, so that they will be incentivized into adopting good research practices. Journals, facing the risk of their track record of publication bias being exposed, should start accepting Null results under the risk of losing readership because of a bad replication index.
- How would SKY edit knowledge? My idea is that whole communities should vet the meta-analysis that concerns them. In practice, that means that the plan for the meta-analysis will be pre-registered on SKY, the code and data will be uploaded as well, and an interface for discussion will be in place. I imagine that interface to be close to the forum of contributors of a Wikipedia page, but with GitHub-like facilities, so that one can easily access the changes implied by an alternative analysis and code. The discussion among the contributors will go-on as long as necessary. The editor in charge of the meta-analysis will be responsible for the final product, but it might be subject to changes, depending on the results of the discussion.
- Do you intend SKY only for economics research or for all types of social science research? To me, the social or behavioral sciences are a whole: they are the sciences that are trying to explain human behavior. SKY will be open to everyone from psychology, economics, medecine, political science, anthropology, sociology, as long as the format of is one using quantitative empirical methods. It might be great eventually to add a qualitative research component to SKY, and a users portion for policy-makers for example, where they could submit topics of interest for them.
- What about methodological research and standardization of empirical practice on SKY? Yep, that will be up there. Any new method will be vetted independently on simulated data, mostly by PhD students as part of their methods class. I'll start by providing my own methods class with its simulations, but then anyone proposing a new method be added to SKY will provide simulations and code so that it can be vetted. We will also provide the most advanced set of guidelines possible in view of the accumulated methodological knowledge.
- Once we have SKY, do we really need journals? Actually, I'm not sure. Journals edit content, providing you with the most important up-to-date results according to a team of editors. SKY does better: it gives you the accumulated knowledge of whole research communities. Why would you care for the latest flashy results, whose contribution to the literature will be to push the average meta-analysed effect in a certain direction by a very limited amount? Of course, super novel results will open up new interpretations, or connect dots between different strands of the literatures, or identify regularities (sets of conditions where effects differ) and confirm them experimentally. But the incentive of researchers will be to report these result in the place where everyone is looking: SKY. Why run the risk of having one's impact limited by paywalls?
- How do you measure the contributions of scientists and allocate research funds in the absence of the hierarchies accompanying journals? That's the best part: SKY will make this so easy. Researchers with a clean record contributing a lot to a meta-analyzed effect (by conducting a lot of studies or one a large one) will be rewarded. Researchers opening up new fields or finding new connections and/or regularities will be easy to spot. Funding will be made easy as well: just look for the most important unanswered questions on SKY. Actually, researchers should after some time be able to coordinate within a community in order to launch large projects to tackle important questions in large teams, just like physicists do.
- Why are you, Sylvain, doing that? While the vision for SKY comes from Chris Chambers' book on the 7 Sins of Psychological Research, I feel this is the most important thing that I can do with my life right now. My scientific contributions will always be parasited and made almost inconsequential in the current system: (i) I cannot identify important questions because I do not know what we know; (ii) I cannot make my contributions known rigorously because Null results get ditched (there are so many more useful things I could be doing with my life right now, and apply my brains, motivation and energy to, rather than publishing biased results and contributing to polluting the published empirical record); (iii) Organizing the published empirical knowledge has a much higher impact on society than conducting another study, because the sample size of literatures is much larger than the one of a given study, so that the precision and impact of the accumulated knowledge will be huge; (iv) I love science, have always done since I was a kid, and I know that it has the power to make the world a better place. I want to contribute to that by nudging science in the right direction to achieve just that. There are so many useful theories and empirical facts in economics and social science that could be of use to everyone if only they had been properly vetted and organized; (v) I am lucky enough to have an employer that really cares about the public good and that supports me 100%. Lucky me :)
- How can I contribute to SKY? Well, drop me an email or a DM on twitter if you want to get involved. We are just starting looking at the solutions and goals, so now is the best time to make a lasting impact on the infrastructure. We will need any single one of your contributions.
With SKY, I want to achieve what Paul Krugman asks economists to do in a recent post: "The important thing is to be aware of what we do know, and why." Couldn't agree more. Let's get to work ;)